Some children are reluctant students of mathematics; they’re not interested in learning equations they don’t think they’ll ever have a use for. I find there’s something magical, however, in plugging numbers into an equation and coming up with an answer – like solving a puzzle!
The inspiration for this blog was seeing an example of how understanding a mathematical equation was key to improving the profitability of a kraft pulp mill, which I’ll get to later. First, let’s discuss some well-known equations that are useful to the pulp and paper industry. And maybe I’ll inspire some of those reluctant schoolchildren to become engineers one day!
One of the oldest equations is the relation of the circumference of a circle to its diameter. Ahmes, an Egyptian scribe, recorded his theory on a papyrus scroll about 1650 B.C. that this ratio was 256/81, or about 3.16. This evolved into C=πd, the area of a circle A=πr2 and the volume of a cylinder V=πr2h, which is how we calculate the volume of a cylindrical tank in a pulp mill, and therefore how long pulp is stored in the tank.
Equations are initially developed by observation or experience. The technical term for this is “empirically”. Empirical equations use experimental data to predict another parameter. Unlike geometric equations such as that proven by Pythagoras for the sides of a right-angle triangle (a2+b2=c2), an empirical equation cannot be considered strictly true, since it can’t be proven true or false by using experimental data. However, the proof of an empirical equation is in its widespread use.
One special type of empirical equation is a calibration curve. We measure one thing (such as the amount of light absorbed by a solution) and it gives us another (such as concentration). Most of these are linear, with an equation y=mx+b. Most sensors in a pulp and paper mill measure properties indirectly by the use of a calibration line or curve.
A useful equation that can be used in papermaking is the Kubelka-Munk equation, developed in 1931. This is a theory that considers the brightness of a surface to be due to two components: the absorption of light that produces colour (less colour = higher brightness) and the scattering of light (by reflection off air-to solid interfaces). It is stated as:
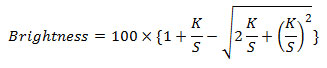
where K and S are absorption and scattering coefficients, respectively, whose values can be determined by laboratory methods. In a mixture, these coefficients are the weighted sum of the coefficients of the ingredients. Thus, if your goal is to maximize the brightness of a sheet of paper, the cost of bleaching (lowering the absorption coefficient) can be compared with the cost of adding a filler such as titanium dioxide (increasing the scattering coefficient) by use of the Kubelka-Munk equation.
Now let’s jump to artificial intelligence. Modern pulp and paper mills simultaneously measure thousands of variables at various time intervals, and “soft” or “virtual” sensors can predict the value of one unknown parameter by using a combination of a selection of measurements. Most commonly these are built by a multivariate PLS (partial least squares) technique, finding the best straight-line relationships between a Y value and several X values. When some or all of the relationships are non-linear, another commonly used technique is neural networks. Increasingly, pulp and paper mills are using these two techniques to build models that are then harnessed to control the input parameters of a process in order to obtain a desired outcome, with the help of powerful computers.
At the recent virtual PacWest meeting bringing together the western Canadian pulp and paper community, the award for the best presentation was given to Ralph Lunn of Mercer Celgar. He used a pair of empirical equations developed in the 1970s by John Tasman for kraft pulp yield and kappa number (lignin content) as a function of H-factor (time and temperature), EA (effective alkali) and S (sulfidity). Those equations are:
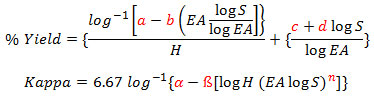
where the values of the constants denoted in red (a, b, c, d, α, ß, and n) depend on the wood species. Wow – these are pretty complicated equations, but Tasman had worked out the values of all the constants for many Canadian softwoods, and of the seven wood species used at Celgar, only a, b, c, and d were missing for hemlock. FPInnovations was able to determine these constants by carrying out labwork for Mercer. To turn this into practical information, Lunn used these equations to work out that, in theory, he could increase the average yield by about 0.44% by operating at a higher sulfidity and a lower EA, resulting in having to buy about 10,000 tonnes less wood chips in a year for his mill. What a great example of using the power of mathematical equations to provide practical information!
 Martin Fairbank, Ph.D. Martin Fairbank has worked in the forest products industry for 31 years,
Martin Fairbank, Ph.D. Martin Fairbank has worked in the forest products industry for 31 years,
including many years for a pulp and paper producer and two years with
Natural Resources Canada. With a Ph.D. in chemistry and experience in
process improvement, product development, energy management and lean
manufacturing, Martin currently works as an independent consultant,
based in Montreal. He is also an author, having recently published
Resolute Roots, a history of Resolute Forest Products and its
predecessors over the last 200 years.
Martin Fairbank Consulting
Industry Experience
- Pulp and Paper Technology
- Materials Recycling
- Biorefinery Development
- Manufacturing
- Government Subsidy Programs
Services
- Technical Writing
. White Papers
. Grant Applications
. Explain technical concepts - Scientific Editing
. Review of articles for publication - Project Assessment
. Evaluation of Technologies
. Project evaluation for funding agencies - Pulp & Paper
. Conventional and emerging technologies













